Lab 2.2 - 3D Projective Geometry and Stereo Reconstruction

Overview

In this lab you’ll learn about 3D projective geometry and stereo reconstruction.

Important: You can obtain 2 bonus marks for each section you finish and demo while present during the lab period we introduce the lab.

1. Homogeneous Transforms and Projections (30)

A transformatrion matrix, \(M\), can be used to transform 3D points in homogeneous form:

\begin{equation} \left(\begin{array}{l} \displaylines{x’\\ y’\\ z’\\w’} \end{array}\right) = M \left(\begin{array}{l} \displaylines{x\\ y\\ z\\1} \end{array}\right) \end{equation}

We define translation and rotation matricies in homogenenous coordinates as follows:

\begin{equation} T=\left[\begin{array}{cccc} \displaylines{ 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1 } \end{array}\right] \end{equation}

\begin{equation} R = R_zR_yR_x \end{equation}

\begin{equation} R_z=\left[\begin{array}{cccc} \displaylines{ cos\theta & -sin\theta & 0 & 0\\ sin\theta & cos\theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 } \end{array}\right] \end{equation}

\begin{equation} R_y=\left[\begin{array}{cccc} \displaylines{ cos\theta & 0 & sin\theta & 0\\ 0 & 1 & 0 & 0\\ -sin\theta & 0 & cos\theta & 0\\ 0 & 0 & 0 & 1 } \end{array}\right] \end{equation}

\begin{equation} R_x=\left[\begin{array}{cccc} \displaylines{ 1 & 0 & 0 & 0\\ 0 & cos\theta & -sin\theta & 0\\ 0 & sin\theta & cos\theta & 0\\ 0 & 0 & 0 & 1 } \end{array}\right] \end{equation}

\begin{equation} S=\left[\begin{array}{cccc} \displaylines{ s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 } \end{array}\right] \end{equation}

a) Generating 3D Point Clouds

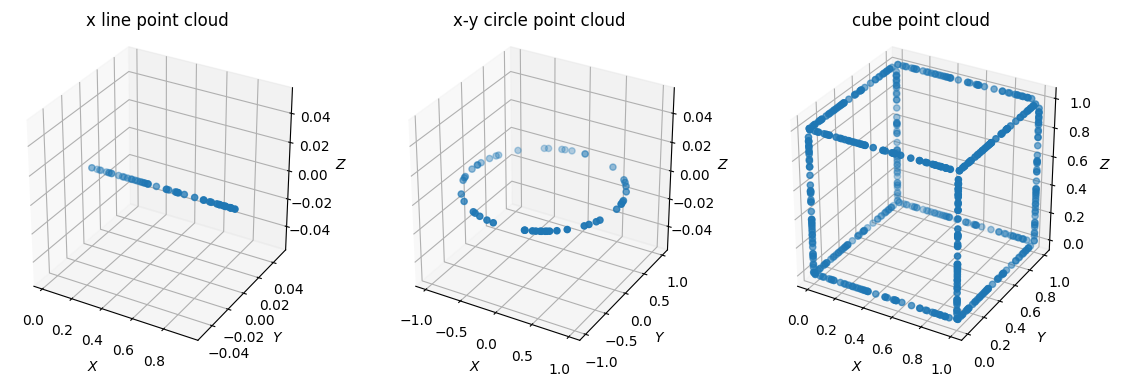
The following code block creates a line with randomly sampled points from \(X\sim U(0,1)\).

import matplotlib.pyplot as plt
import numpy as np

numpoints = 50
t = np.random.rand(1, numpoints)
zeros = np.zeros((1, numpoints))
ones = np.ones((1, numpoints))

x_l = t
y_l = zeros
z_l = zeros
line = np.row_stack((x_l, y_l, z_l, ones))
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.set_box_aspect([1,1,1])
ax.scatter(x_l, y_l, z_l, 'gray')
plt.title("x line point cloud")

• Recreate the plots above featuring a line, a circle, and a cube.

Deliverables:

• Display your figure in your report.
• Save your figure to include in your submission.

Report Question 1a: What type of projection is being used to render these point clouds on our screen?

b) 3D Homogeneous Transformations

• Create functions that return the 3D transformation matrices defined above. Use them to apply the following transformations on your cube point cloud:
  1. A rotation about at least two axes.
  2. A translation and a scaling.
  3. Create an equally-spaced facade of 4 cubes. Apply one rotation and scaling operation of your choice to all 4 cubes.

Deliverables:

• Display figures of your transformed cubes in your report.
• Save figures of your transformed cubes to include with your submission.

Report Question 1b: In what situations do rotations also translate the cube?

c) Projections

1. Apply orthographic projection to the first two transformed cube point clouds you created in b)
2. Apply perspective projection to the first two transformed cube point clouds you created in b)

Deliverables:

• Display your four projections in your report.
• Save your four projections to include with your submission.

Report Question 1c: Name two differences between orthographic projection and perspective projection.

d) Bonus (10) - Animation

• Create an animation using transformations and projections you’ve learned in this course thus far. First, create the animation in 3D and then project it to 2D.
• If you wish to place your animation into a scene, you must recover the camera matrix given a set of 2D and 3D point correspondences by modifying your DLT algorithm (see page 54-62 of these slides)
  • This is not mandatory, but it is the mechanism that allows for your projections to “match” a scene. The cover video for this page was created in this manner.
• Be creative! An additional 5 bonus marks will be awarded cool-factor, as judged by the TAs. Minimal marks will be awarded for trivial animations.

Deliverables:

• Save the animation to include with your submission

Report Question 1d: Briefly describe how you created your animation.

2. Estimating Focal Length (10)

• Determine the focal length of your phone camera by using it to take a picture of a ruler a known depth away.
• Make sure the ruler is placed perpendicular to the camera axis (i.e. the ruler is square to the camera).
• Use similar triangles formed with the ruler and its projection in the image to find your camera’s focal length in pixels (See page 68-72 of these slides.
• Convert the focal length to mm using the ratio of our photo’s width in pixels to your phone’s camera sensor width in mm.
• Convert the focal length in mm to its full-frame equivalent by using the diagonal sensor width ratios between your phone camera and a 35 mm film camera, also known as the crop factor (reference the crop factor of your camera sensor in this table)

Deliverables:

• Write the focal length in pixels and mm (full-frame equivalent) and the manufacturer’s specified focal length as a comment in your code.
• Write the focal length in pixels and mm (full-frame equivalent) and the manufacturer’s specified focal length in your report.

Report Question 2 What is the focal length of your phone camera? How does this compare to the manufacturers’ specifications?

3 SSD-based Stereo Depth Estimation (20)

Implement a window-based Sum of Squared Differences (SSD) method for stereo matching to compute a disparity map. Then, convert it to a depth map using known camera parameters.

a) Disparity Map Computation (SSD):

• You are provided the calibrated Tsukuba stereo pair (left and right images) with the following camera parameters:
  • Focal Length: \(f = 300\) pixels
  • Baseline: \(B = 0.16\) meters
• Write a program that implements the SSD method for computing disparity:
  • For each pixel in the left image, extract a square window of size \((2w+1) \times (2w+1)\) (e.g. \(w=3\) for a 7×7 window).
  • For each candidate disparity \(d\) in a specified range (e.g. from \(-d_{\text{max}}\) to \(d_{\text{max}}\)), compute the matching cost using the formula:

$$ \text{SSD}(x, y, d) = \sum_{i=-w}^{w} \sum_{j=-w}^{w} \left[ I_L(x+i, \, y+j) - I_R(x+i-d, \, y+j) \right]^2 $$

• Select the disparity \(d^*(x,y)\) that minimizes the SSD for each pixel.

Report Question 3a:

• How do the choices of window size and disparity search range affect the accuracy and noise level of your disparity and depth maps? What are the potential limitations of using the SSD approach, especially in textureless or occluded regions?
• In the tracking lab you had the option of implementing a pyramidal tracker; could a similar pyramidal strategy be used here to increase performance? How would it work?

Deliverables:

• Save the the disparity map to include with your submission.
• Place the disparity map in your report.

b) Depth Map Computation:

• Convert the computed disparity map \(d^*(x,y)\) to a depth map using the stereo geometry relationship:

$$ Z(x,y) = \frac{f \cdot B}{|d^*(x,y)|} $$

• Hint: Refer to pages 12-14 of these slides for guidance on the depth computation process.

• Be sure to handle cases where the disparity is zero or nearly zero (e.g., by thresholding or marking these pixels as invalid).

• Bonus (5) - Modify your program to apply a simple smoothing or median filter to the disparity map before converting it to depth. In your report, explain how this post-processing step improves (or degrades) the quality of the final 3D reconstruction.

Report Question 3b: Would our reconstruction still work if the translation is not perpendicular to the camera axis?

Deliverables:

• Save the the depth map to include with your submission.
• Place the depth map in your report.

4. 2-Image Stereo Reconstruction (15)

In this question you will use point correspondence to perform 3D reconstruction. You will work with your own camera and calculated camera parameters to determine the depth of the feature points. Reconstruct the 3D coordinates in a camera-centered coordinate system, and texture your 3D model.

1. Image Acquisition:
   • Setup: Place a camera perpendicular to a ruler pointed at a box object.
   • Capture: Take an image of the object.
   • Shift and Capture Again: Move the camera laterally by a known distance (measured by the ruler) and take a second picture.
2. Feature Correspondence:
   • Select the corner points (or other feature points) in both images to create a set of corresponding feature points.
3. Depth Computation:
   • Determine the depth of the feature points. This should be the same as you did in question 3.
     Hint: Refer to pages 12-14 of these slides for guidance on the depth computation process.
4. 3D Reconstruction:
   • Use the computed depths to reconstruct the 3D coordinates of the feature points in a camera-centered coordinate system.
   • Plot the reconstructed points in a 3D plot.
5. Texture:
   • Texture your 3D object. For example, texture rectangular faces by calling plot_surface() for each face (See plot_surface() example).

Report Question 4: Would our reconstruction still work if the translation is not perpendicular to the camera axis?

Deliverables:

• Save and include the 3D plot of the reconstructed object.
• Save and include the two images you captured.
• Incorporate these results in your final report.

5. n-Image Stereo Reconstruction (25)

In this section you will extend your 2-image stereo reconstruction pipeline to handle multiple images (\(n\) images). You will work either synthetic data or real data captured by you.

a) n-Image Stereo Reconstruction

1. 3D Object Creation:
   • Build a 3D representation of a box object.
2. Projection onto Multiple Images:
   • Project the 3D structure onto a set of \(n = 10\) images.
   • Camera Setup: Assume the images are taken along a line perpendicular to the camera axis at fixed intervals.
   • Perspective Projection: Use a camera with the focal length determined in Question 2 to perform the projection.
3. Depth Determination with Multiple Views:
   • Formulate a least squares system to determine the depth of the feature points using all \(n\) images.
   • Reconstruct the 3D coordinates and compare the results with your original 3D structure.
4. Texture:
   • Texture your 3D object by applying plot_surface() to texture each rectangular face (See plot_surface() example).

Deliverables:

• Save and include the 3D plot of the reconstructed object.
• Save and include one example projection image.
• Add these results to your report.

Report Question 5a: How does the reconstruction process differ as we increase the number of images in our dataset?

b) Bonus (15) - Real Data

1. Video Acquisition:
   • Record a video of a moving object (or a moving camera) along a line perpendicular to the camera axis.
     Note: Sliding your object/camera against a fixed surface can improve recording quality.
2. Feature Tracking:
   • Use a tracker to follow a set of feature points that characterize the object’s structure throughout the video (e.g., the corners of a box).
3. Depth Computation with Multiple Views:
   • Formulate a least squares system to determine the depth of the feature points using all frames (treated as individual images) from the video.
   • Reconstruct the 3D coordinates and compare the results with the starting structure.
4. Texture:
   • Texture your 3D object by applying plot_surface() for each face (See plot_surface() example).

Deliverables:

• Save and include the 3D plot of the reconstructed object.
• Save and include the recording (video) used for the reconstruction.
• Include one representative frame from the video with the features you tracked marked in your final report.

Submission Details

• Include accompanying code used to complete each question. Ensure they are adequately commented.
• Ensure all functions are and sections are clearly labeled in your report to match the tasks and deliverables outlined in the lab.
• Organize files as follows:
  • code/ folder containing all scripts used in the assignment.
  • media/ folder for images, videos, and results.
• Final submission format: a single zip file named CompVisW25_lab2.2_lastname_firstname.zip containing the above structure.
• Your combined report for Lab 2.1 and 2.2 is due shortly after (see calendar for details). The report contains all media, results, and answers as specified in the instructions above. Ensure your answers are concise and directly address the questions.
• Total marks for this lab is 100 for all students. Your lab assignment grade with bonus marks is capped at 130%.