Lab 1.1 Optical Flow
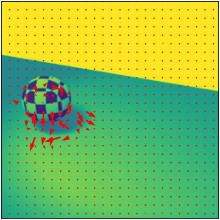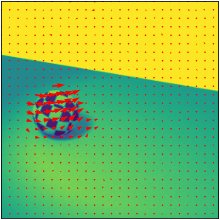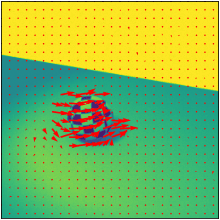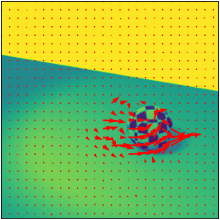
Overview
In this lab, you’ll implement a basic 2-DoF optical flow algorithm. These flow vectors describe the motion in a scene. Equation 1 is the basis of optical flow. We can capture the temporal shift between two frames by using a first order approximation:
\begin{equation} -I_t=\nabla I^T\mathbf{u} \end{equation}
where \(I_t\) is the temporal gradient, and \(\nabla I^T=\left[I_x,\ I_y\right]\) is the spatial gradient. For each image in our sequence, we want to find its temporal and spatial gradients and solve for \(\mathbf{u}\).
This zip file contains the sample videos you can use to complete this lab. However, you are encouraged to capture your own and evaluate which videos perform well and which perform poorly.
Lab Introduction Slides: available here
Important: You can obtain 2 bonus marks for each section you finish and demo while present during the lab period we introduce the lab.
Prelab Questions (5%)
The link to the prelab questions can be found here. You will need your University of Alberta email for access; they are also available under the Canvas assignment. Due Tuesday, January 13 at 5pm.
Setup
First, download the lab code and report templates. These contain the structure for your report, and the file structure for your code. You can write your code however you wish within the files; however, please ensure that it is adequately commented, and that each part of the lab can be run by running the file corresponding to that question.
You will need to use your University of Alberta email to access the below templates.
Code template: can be found here.
Report template: can be found here.
0. Capturing Images with OpenCV
The following code grabs frames from a camera and displays them in a new window:
import cv2
cam = cv2.VideoCapture(0, cv2.CAP_FIREWIRE) # Remove second arg if using webcam
while True:
ret_val, img = cam.read()
cv2.imshow('test', img)
Modify this code to use imwrite to save a sequence of images we will use for this lab.
1. Single Window Optical Flow (20)
Write your code for this section in the q1_single_window_optic_flow.py file.
Complete the following steps for a single image pair:
a) Temporal Image Gradient
- Convert a sequenced pair of images to grayscale.
- Find the temporal difference between the two images.
- Threshold the temporal derivative by setting values that do not meet our threshold to zero.
- Test different threshold values until motion is isolated and noise is minimized.
Deliverables:
- Display the final thresholded temporal derivative in your report.
Report Question 1a: What does the temporal image gradient tell us about our image pair?
b) Spatial Image Gradient
- Write a function that finds the spatial image gradients, \(I_x\) and \(I_y\), along the first and zeroth axes of our image, respectively. Compute an approximation of \(I_x\) and \(I_y\) using the definition of a gradient. Avoid using
numpy.gradientfor this exercise.
Deliverables:
- Display \(I_x\) and \(I_y\) as images in your report using your image pair.
Report Question 1b:
- What features are prominent in each spatial gradient?
- Report Bonus (2) Include examples of images with prominent features and images without prominent features. How does this affect things like the condition number of the image and subsequently the quality of the computed (u)?
c) Solve for \(\mathbf{u}=[u,v]^T\)
- Plot \(\mathbf{u}\) onto the center of our image using
matplotlib.pyplot.quiver.
Deliverables:
- Display the calculated flow vector on your image in your report using the same image pair as in step 1 and 2.
2. Single Window Live Optical Flow (20)
Write your code for this section in the q2_single_window_live_optic_flow.py file.
- Now, extend your code from question 1 to show single window optical flow on a live video. Code in Question 0 gives the structure to retrieve live frames. Use this with your code above to show optical flow on a video stream.
Deliverables:
- Save a video of single window flow with the overlaid motion vectors to include in your submission. Please place this in a folder called
media. Ensure the video is less than 10 mb.
Report Question 2: What is one limitation of finding a single optical flow vector on the entire window?
3. Optical Flow on Patches using Image Pairs (20)
Write your code for this section in the q3_optic_flow_patches.py file.
Complete the following steps for one timestep:
- Divide your gradients into patches of size
block_size x block_size. - For each patch, find the flow vectors \(u\) and \(v\).
- For each tile, plot the motion vector \(\mathbf{u}\) onto the center of the tile using
matplotlib.pyplot.quiver.
Report Question 3a: How does changing block_size affect your results? What are some benefits and drawbacks of increasing block_size?
Report Question 3b: What sort of motion have we captured here? Name two types of motion we cannot account for with our current method.
Deliverables:
- Display the flow vectors for one image pair/timestep in your report.
4. Live Optical Flow (20)
Write your code for this section in the q4_live_optic_flow.py file.
a) Implement a live implementation of optical flow with patches.
- Modify your code in question 3 to run on a live video feed.
- Explore what video characteristics enable good or bad performance for our algorithm.
Report Question 4a: Name three assumptions we make for optical flow to work.
b) Capture one video that results in ideal performance for your optical flow algorithm.
- Apply your optical flow function to the video.
Deliverables:
- Save the video with motion vectors to include in your submission. Please put it in a folder
media/good. Ensure the video is less than 10 mb.
Report Question 4b: Why is this video suitable? Relate your answer to the assumptions named in Report Question 2a.
c) Capture one video that results in poor performance for your optical flow algorithm
- Apply your optical flow function to the video. You may artificially generate a non-trivial video for this question.
Deliverables:
- Save the video with motion vectors to include in your submission. Please put it in a folder
media/bad. Ensure each video is less than 10 mb.
Report Question 4c: Why is this video unsuitable? What assumptions does your video violate?
5. Rotation and Scale (20)
This question is a bonus for undergraduate students.
Grad students: this question is mandatory.
Write your code for this section in the q5_rotation_scale_gradients.py file.
a) Rotation and Scale Gradients
- Write a function to find rotation and scale gradients \(I_r\) and \(I_s\) for a single image.
Deliverables:
- Plot the rotation and scale gradients for an image in your report.
b) Solve Motion Vectors for Rotation and Scale
- Write a function to solve for motion vectors \(r\) and \(s\) using a formulation similar to Equation 1 in a single window (i.e., no tiles) of a video with rotation and zoom with respect to the camera axis.
- Plot your results by mapping the x-vector to rotation and the y-vector to scale.
Deliverables:
- Save your plotted rotation and scale vector results in your report.
- Report Bonus (2) Include examples of images with prominent features and images without prominent features. How do these differ from the prominent features you found in \(I_x\) and \(I_y\)?
Submission Details
- Include accompanying code used to complete each question. Ensure they are adequately commented.
- Ensure all functions and sections are clearly labeled in your report to match the tasks and deliverables outlined in the lab.
- Organize files as follows, using the provided template:
-
code/folder containing all scripts used in the assignment. -
media/folder for images, videos, and results.
-
- Final submission format: a single zip file named
CompVisW26_lab1.1_lastname_firstname.zipcontaining the above structure. - Your combined report for Lab 1.1 and 1.2 is to be submitted at the end of the topic at a later date. The report contains all media, results, and answers as specified in the instructions above. Ensure your answers are concise and directly address the questions.
- Total marks for this lab is 80 for undergraduate students and 100 for graduate students. Your lab assignment grade with bonus marks is capped at 110%. Report bonus marks will be applied to the report grade, also capped at 110%. Bonus marks can only be obtained if all non-bonus questions are completed.