X-ray imaging, as well as many other imaging methods are based on
measuring the attenuation of a medium. In a simple conventional
X-ray image, all attenuation between the X-ray source and camera
is integrated into a 2D image. Because some structure attenuates more
than other, a doctor can examine structures (e.g. bone in the body,
caries decay in teeth). However, as described the method essentially
projects and ``blurs'' the true 3D structure onto a 2D plane.
In tomography, or CT-scanning (from Computer Tomography), a computational
process is used to uncover a 3D image from multiple 2D images. The following
is a short description for those who want a bit of technical background.
For those eager to get to the implementation, all that is needed for that
is described in the next section. You can also learn more starting
from e.g. the following wikipedia links:
Computed tomography
Tomographic reconstruction
A discrete 3D image is represented by small volume elements voxels.
Here, without loss of generality we will develop the theory for one
axial slice of voxels, which then akin to in a normal 2D image are
named pixels. The whole 3D image is then simply composed of
several such slices stacked up.
Figure 1:
Tomography machine and working principle
|
|
The principle enabling 3D reconstruction is to detect the x-ray absorption
along numerous sets of rays going through a body, as shown in Fig 1. In
practice this kind of apparatus is built by rotating a diametrically opposed
X-ray source and detector. Fig. 2 shows the typical design of a hospital
CT machine. The xray source and detectors are built into the circular
structure, and the patient is inserted into the central opening.
Each ray measures the cumulative attenuation along a line. In the
discrete representation, this line intersects several pixels, as shown in
Fig. 3 and 4. Hence from the signal of one detector we only know
the combined attenuation of all pixels along that ray. The X-ray absorption
density in pixel 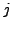 is defined as
is defined as
Where 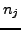 is the number of incoming photons and
is the number of incoming photons and 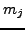 is the number of
outgoing photons leaving pixel
is the number of
outgoing photons leaving pixel 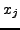 . Now if a ray intersects several
pixels, say pixel
. Now if a ray intersects several
pixels, say pixel
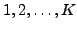 then the total absorption along the
ray is
then the total absorption along the
ray is
To set a reference level 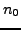 for each X-ray detector, the machine is run
without a person in it. Now the total x-ray absorption along a ray
for each X-ray detector, the machine is run
without a person in it. Now the total x-ray absorption along a ray 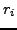 can
be written
can
be written
and each pixel along the ray 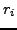 thus contributes additively as
follows
thus contributes additively as
follows
Now we want to recover the 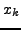 , and to do so we have to take
a sufficient number of rays intersecting different subsets of pixels,
then form an equation system with the measured absorptions
, and to do so we have to take
a sufficient number of rays intersecting different subsets of pixels,
then form an equation system with the measured absorptions 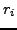 as
righthand sides,
as
righthand sides, 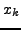 as unknowns, and a matrix of 1's and 0's describing
which pixels are intersected by which ray.
as unknowns, and a matrix of 1's and 0's describing
which pixels are intersected by which ray.
We first consider some simple 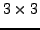 and
and 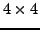 cases, then
a more general
cases, then
a more general 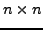 Set up the equation system for pixel 1 to 9 the
Set up the equation system for pixel 1 to 9 the 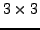 imaging
situation illustrated in the figure below using b-data, where b_i = r_i above. Select a suitable
subset of observations to form a b-vector and A matrix. Pay attention to
that the A matrix has to be full rank for the solution to make sense.
Solve the system using Matlab's built-in LU routine.
Set up and solve the overdetermined system arising from
data 1,2,3 and 4 using Matlab's ``
imaging
situation illustrated in the figure below using b-data, where b_i = r_i above. Select a suitable
subset of observations to form a b-vector and A matrix. Pay attention to
that the A matrix has to be full rank for the solution to make sense.
Solve the system using Matlab's built-in LU routine.
Set up and solve the overdetermined system arising from
data 1,2,3 and 4 using Matlab's `` " operator.
Is this solution better? Why?
" operator.
Is this solution better? Why?
Figure 2:
Tomography pixel line scan patterns
b_1 = 13.00
b_2 = 15.00
b_3 = 8.00
b_4 = 14.79
b_5 = 14.31
b_6 = 3.81
b_7 = 18.00
b_8 = 12.00
b_9 = 6.00
b_10 = 10.51
b_11 = 16.13
b_12 = 7.04
|
|
Extend the above generation to a 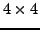 case. Now it becomes less obvious
what are a good set of rays (imaging directions). Explore some different
options and study the rank and numerical conditioning of the matrix.
Use a
case. Now it becomes less obvious
what are a good set of rays (imaging directions). Explore some different
options and study the rank and numerical conditioning of the matrix.
Use a 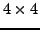 image
image 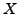 of your own design. Reshape the image into a column vector
of your own design. Reshape the image into a column vector 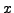 and form the observations
using
and form the observations
using 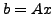 . From this data
. From this data 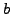 make sure you can reconstruct the image.
make sure you can reconstruct the image.
The 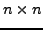 case is a direct generalization of the above small cases.
The main challenges are to construct the matrix correctly (this is avoided in part c1).
We choose a relatively low resolution to make the computation tractable even
with the regular lu or similar routines working on full matrices. However,
matlab can also handle sparse matrices. (optional) If you are interested
you can try this. start with ``help sparfun''. Another alternative is to use an iterative method. There are some examples in the Heath textbook.
case is a direct generalization of the above small cases.
The main challenges are to construct the matrix correctly (this is avoided in part c1).
We choose a relatively low resolution to make the computation tractable even
with the regular lu or similar routines working on full matrices. However,
matlab can also handle sparse matrices. (optional) If you are interested
you can try this. start with ``help sparfun''. Another alternative is to use an iterative method. There are some examples in the Heath textbook.
We have provided the design matrix 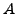 and absorption coefficients
and absorption coefficients 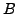 for two particular data setups in
lab1c_part1.mat.
(You can also access this data directly on the ugrad lab computers by ``cd
/cshome/vis/cmput340/lab1cData''.)
Note that each column of
for two particular data setups in
lab1c_part1.mat.
(You can also access this data directly on the ugrad lab computers by ``cd
/cshome/vis/cmput340/lab1cData''.)
Note that each column of 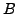 corresponds to a full scan. Solve the system of equations for each column and display
the results using imshow. (Note: the solution gives you a column vector, which you will
need to reshape into a square matrix, using reshape(x,[n,n]). You will also need to
transpose the result, as the data we are dealing with is accessed row-major whereas Matlab
assumes column major). One of the datasets, char_c1.mat, contains a sequence of letters. What
word does it spell out? The other, mri_c1.mat, contains several slices of a brain image as exemplified below.
corresponds to a full scan. Solve the system of equations for each column and display
the results using imshow. (Note: the solution gives you a column vector, which you will
need to reshape into a square matrix, using reshape(x,[n,n]). You will also need to
transpose the result, as the data we are dealing with is accessed row-major whereas Matlab
assumes column major). One of the datasets, char_c1.mat, contains a sequence of letters. What
word does it spell out? The other, mri_c1.mat, contains several slices of a brain image as exemplified below.
Figure:
Example slice of a human brain
|
|
Reconstruct the voxel from the scan data available in
lab1c_part2.mat.
The input data comes in the form of two cell arrays thetas and scans. Element i of the thetas array is an
 column vector containing the rotation angles (in degrees) of the scan head for each scan. Element i of the scans array contains a
column vector containing the rotation angles (in degrees) of the scan head for each scan. Element i of the scans array contains a
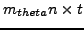 matrix, where each column is the
matrix, where each column is the 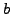 -vector for a full scan, and there are
-vector for a full scan, and there are 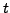 of them (perhaps a sequence of images from the same scanner setup over time). Note that you can extract
of them (perhaps a sequence of images from the same scanner setup over time). Note that you can extract 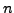 , the size of the voxel grid and scanner head, from the size of
, the size of the voxel grid and scanner head, from the size of  .
.
Figure:
Example setup for 2x2 grid. Rotation is always interpreted around center of image. For this problem,
![$\theta =[0,45]^T$](img31.png) , and each complete scan would be of the form
, and each complete scan would be of the form
![$\vec{b}=[b_1,b_2,b_3,b_4]^T$](img32.png) .
.
|
|
For consistency, assume that a ray intersects a voxel if the center of the voxel is less than 0.55 units from the line. The rotation should be interpreted as in Figure ![[*]](file:/usr/share/latex2html/icons/crossref.png) and the
and the 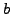 -vector is read from the rays in a consistent manner, where at 0 rotation they align with the center of the voxels along the horizontal scanlines.
-vector is read from the rays in a consistent manner, where at 0 rotation they align with the center of the voxels along the horizontal scanlines.
As illustrated, the imaging is orthographic, with the sensor capturing
a parallel ray set from each angle. At angles [0, 90] degree it is is trivial to
enumerate ray-pixel intersections. Let the intersection of the [0, 90] degree
rays define the pixel centres. Any real camera would have a point spread
function (psf) around
each ideal ray centre. Here the capture window is defined to be 0.55
radius from the line w.r.t. above coordinate system. (ie if rays are 1mm apart
we will have 1x1mm pixels and a ray intersects a pixel is it is within .55 mm
of the ray centre.)
418/501 Numerical Analysis
![\includegraphics[width=1.0\textwidth]{TomoOver}](img1.png)
![]() is defined as
is defined as
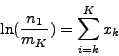
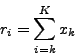
![\includegraphics[width=1.0\textwidth]{TomographyScanPatt}](img18.png)
![\includegraphics[width=0.5\textwidth]{spec}](img33.png)
![]() and the
and the ![]() -vector is read from the rays in a consistent manner, where at 0 rotation they align with the center of the voxels along the horizontal scanlines.
-vector is read from the rays in a consistent manner, where at 0 rotation they align with the center of the voxels along the horizontal scanlines.